Форма зубных дуг человека определяется особенностями расположения зубов, в частности, в переднем сегменте арки, составляющим компонентом которого являются 6 фронтальных зубов [1]. В данном исследовании представлены современные классификации арок зубного ряда, их соразмерность с типологическими вариантами лица и отмечены характерные показатели линейных размеров по всем направлениям, включая диагональные параметры переднего сектора и арки зубных рядов в целом. Несмотря на наличие полового диморфизма размеров зубов, специалисты склоняются к мнению о том, что гендерные и расовые особенности одонтометрических показателей имеют меньшее значение, чем размеры головы и лица и, в частности, его гнатического отдела [2]. Таким образом, вполне закономерно, что длина переднего сектора дуги коррелирует с суммарной величиной ширины коронковых частей резцов и клыков. Большинство исследователей склоняются к мнению, что размеры передних зубов являются ведущим ориентиром при определении радиуса окружности переднего сектора дуги, что к тому же отражено и в исследованиях морфологического плана [3]. В приведенном исследовании также представлены различные классификации дентальных арок у людей с различными видами физиологических и аномальных форм, при которых существенная вариабельность касается переднего отдела обеих зубных арок.
На принципах одонтометрии построена графическая репродукция дуги Хаулея, в которой радиус окружности составляют мезиально-дистальные диаметры коронковых частей двух резцов и клыка одной из сторон верхней челюсти. Учитывая вариабельность размеров симметрично расположенных антимеров и гендерные различия индивидуумов, предложено за радиус окружности Хаулея принимать полусумму ширины коронок шести фронтальных зубов. Для более точного определения радиуса предложен метод его расчета как отношение утроенной длины полусектора (суммы трех зубов) к числу π [4]. Этот показатель основан на закономерностях геометрии круга и несоответствии длины сектора, ограничивающего его, с величиной радиуса окружности переднего сектора арки. Однако при проведении подобных исследований авторами не учитывался трузионный тип зубных арок, который играет решающую роль в оценке расположения зубов переднего сектора арки.
Исследованиями специалистов показана вариабельность переднего сектора, которая определяется не только размерами зубов, но и их ротацией, а также гнатическими (аркадными) типами зубных дуг и различием в торковых (инклинационных) показателях, что отражается на радиусе переднего сектора арки [5]. Данные исследования представлены с цифровыми показателями ротации зубов верхней и нижней арки. Приведены величины углов ротации антимеров для арок зубных рядов различного трузионного типа.
Заслуживает внимания мнение специалистов о влиянии глубины переднего сектора арки и хорды, ограничивающей его и соответствующей межклыковому расстоянию [6]. Отмечено, что при увеличении межклыкового расстояния закономерно уменьшение глубины дуги при одинаковых размерах зубов. И эти величины были приняты авторами за расчет радиуса малого круга. Однако авторы отмечали, что данная методика может быть использована лишь при некоторых типах дуг и требует детального анализа. К тому же линейные параметры, такие как ширина и глубина фронтального отдела, могут быть измерены только при физиологической окклюзии. Тем не менее данный анализ может быть использован в качестве критериальной оценки эффективности лечения аномалий.
В последнее время появляются исследования специалистов, которые указывают на взаимосвязь размеров зубных дуг, в частности на форму переднего сектора, с размерами и морфометрическими особенностями гнатического отдела лица [7].
Специалисты обращают внимание на взаимозависимость размеров арок зубных рядов в сагиттальном направлении с широтными показателями [8]. Однако в данной работе приведены сведения о верхней челюсти и требуются дополнительные наблюдения по закономерностям исследуемых величин нижнего зубного ряда.
Предложенные алгоритмы оценки соответствия типов лица и зубных дуг лежат в основе диагностических мероприятий в ортодонтии и построении зубных дуг в съемных конструкциях зубных протезов [9, 10]. Однако данные методы были рассмотрены для анализа только верхних дентальных арок, как и другие наблюдения специалистов.
Комплексный анализ зависимости формы дентальных дуг от данных одонтометрии показан у людей с различными типами лица. При этом определены варианты макро- и микродонтизма и отмечено их влияние на положение передних зубов в передне-заднем направлении, что отражается на кривизне дуги переднего сектора арки [11]. В данной работе уделено внимание типологическим особенностям лица и зубных дуг и показаны критерии определения их соответствия.
При определении параметров мандибулярных арок оценивается величина условного суставного треугольника по данным конусно-лучевой томографии (КЛКТ) на рентгенологических срезах, проведенных на различных уровнях [12]. В данной работе представлена методика измерения томограмм височно-нижнечелюстного сустава и отмечена вариабельность размеров костных структур. Выделены типы суставной ямки, различающиеся по высоте и передне-заднему размеру. Отмечено, что узкие и высокие параметры ямки, как правило, соответствовали ретрузии резцов с физиологическим резцовым перекрытием. Для протрузионных физиологических вариантов положения резцов была характерна низкая по высоте, но удлиненная в сагиттальном направлении форма ямки. Также представлены особенности межрезцового угла, характеризующие типологические особенности трузионных типов арок дентальных рядов.
К аналогичному мнению пришли специалисты, оценивающие значение КЛКТ в изучении анатомической изменчивости черепно-лицевого комплекса [13]. В периоде прикуса молочных зубов форма зубной дуги по методике Шварца очерчивается в виде полуокружности, диаметром которой является ширина заднего отдела арки, измеряемая между вторыми молярами. Не исключена возможность определения радиуса дуги с учетом размеров челюстно-лицевой области [14]. В данной работе основу графического анализа составляла суммарная составляющая всех зубов верхней арки.
Наиболее сложным в клинической ортодонтии является определение радиуса переднего сектора дуги при асимметричных формах, этиологией которых является неравенство количественного состава антимеров [15]. При данных патологических формах арок наиболее сложным является определение центральной (или, как еще ее называют, межрезцовой) точки дуги, которая, как правило, смещена в сторону с меньшим количеством зубов.
Учитывая многообразие методов построения зубных дуг, авторы приняли решение о проведении сравнительного анализа различных методов построения окружности, что определило актуальность и цель предстоящей работы. Цель исследования – провести сравнительный анализ различных методов определения радиуса окружности для расположения передних зубов и возможности их применения в клинической ортодонтии.
Материалы и методы исследования
С учетом рекомендаций специалистов 54 пары моделей челюстей из гипса, соответствующие физиологической окклюзии, оцениваемой по шести ключам Эндрюса, были разделены на три группы с учетом трузионного типа. В первой группе было 28 пар моделей с вариантами мезотрузии передних зубов. Во вторую группу входило 14 пар моделей с вариантами физиологической ретрузии. В третьей группе было 12 пар моделей, относящихся к протрузионному типу. Модели челюстей принадлежали молодым людям в возрасте от 18 до 25 лет.
Типологические особенности определяли по расположению резцов обеих челюстей с помощью прибора фирмы Шой-Дентл (Германия). На предметном столике, установленном горизонтально по встроенному уровню, оценивали наклон зубов в передне-лингвальном направлении, что определяло торк или инклинацию зубов. Прибор позволял определить и ангуляционный наклон зубов при необходимости. Отклонение вестибулярной поверхности центральных верхних резцов на 10–15° определяло принадлежность к мезотрузионному варианту. Изменение показателя в большую сторону свидетельствовало о протрузионном типе арок и «высоком» торке исследуемых органов. Величина угла менее 9° была характерна для ретрузии центральных резцов. При этом торковые показатели зубов соответствовали «низким» значениям торка.
Хрестоматийный метод Хаулея – Гербера – Гербста для построения графической репродукции дуги основывался на том, что радиус малого круга соответствовал суммарной ширине коронок резцов и клыка одной из сторон дентальной арки (классический радиус Хаулея). После построения окружности, из верхней ее точки тем же радиусом откладывали ориентиры на круг, которые указывали на место расположения клыков верхней арки. Данный метод подробно описан практически во всех учебниках и пособиях по ортодонтии и не требует детального представления.
При втором варианте построения окружности, по которой должны размещаться 6 передних зубов, радиус рассчитывался по отношению тройной величины радиуса Хаулея к числу π (модифицированный радиус Хаулея). Данный метод позволял избежать погрешности в определении радиуса окружности для построения дуги Хаулея и подчеркивал неравенство хорды сегмента (соответствующей величине радиуса круга), его длине (сумме трех зубов), что вполне логично с точки зрения законов геометрии круга, так как длина дуги всегда больше хорды.
Третий вариант расчета радиуса проводился по методике Ярадайкиной, в которой радиус окружности составлял разницу между клыковым расстоянием и глубиной переднего сектора арки. Данный метод показывал зависимость величины хорды от глубины дуги переднего сектора.
а) 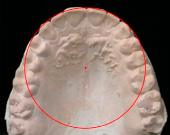
б) 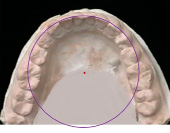
Фотографии гипсовых моделей верхней (а) и нижней (б) челюсти с нанесенным контуром круга для оценки расположения шести передних зубов
Четвертый метод расчета радиуса проводился с учетом закономерностей геометрии круга, в котором передний сектор был ограничен хордой, соответствующей расстоянию между рвущими бугорками клыков, а его глубина соответствовала глубине переднего отдела зубной арки. Расчет производили по формуле, которая включала в себя дробь, в числителе которой была сумма квадратов ширины и глубины арки, а в знаменателе была удвоенная величина глубины переднего сектора дуги (метод построения круга по параметрам переднего сектора). При этом глубина передней части арки определялась через синус угла, образованного резцово-клыковой диагональю и условной линией межклыковой трансверсали. При мезотрузии резцово-клыковый угол верхней арки составлял 25°, на нижней – 20°. Протрузионный тип арок характеризовался тем, что величина указанного угла верхней челюсти составляла 30° и глубина дуги была вдвое меньше передней диагонали (синус 30° равен 0,5). На нижней дуге угол был в пределах 25°. Ретрузионный тип характеризовался величиной резцово-клыкового верхнего угла в 20°, а нижнего – в 15°.
В качестве контроля нами предложен метод фотостатического исследования зубных дуг (рисунок).
При этом на фотографию модели в окклюзионной проекции накладывали контур окружности и измеряли радиус. Полученный фактический радиус круга сравнивали с различными расчетными величинами в каждой группе исследования. Результаты измерений оценивали статистически с использованием программного обеспечения таблиц Microsoft Excel.
Результаты исследования и их обсуждение
В результате фотостатического метода построения круга было выявлено, что его радиус в среднем по группе с мезотрузионными вариантами зубных арок составил для верхней челюсти 23,31±0,19 мм. При ретрузионных вариантах дуг радиус окружности был достоверно больше и составлял 25,83±0,33 мм (р ˂ 0,05). В то же время на моделях протрузионного типа радиус круга был достоверно меньше, чем в других группах моделей челюстей, и составлял 20,25±0,24 мм (р ˂ 0,05).
На нижней челюсти исследуемые показатели для арок мезо-, ре- и протрузионного типа составляли соответственно 21,50±0,26; 25,10±0,25 и 18,51±0,19 мм с достоверностью различий между всеми показателями (р ˂ 0,05).
При построении круга по классическому методу Хаулея было выявлено, что его радиус в среднем по группе с мезотрузионными вариантами зубных арок составил для верхней челюсти 23,07±0,65 мм. При ретрузионных вариантах дуг радиус окружности составлял 22,26±0,45 мм. В то же время при расчете для протрузионного типа радиус составлял 24,30±0,98 мм, и достоверных различий между показателями не отмечено, что обусловлено тем, что данные одонтометрии практически не отличались между группами наблюдений. На нижней челюсти исследуемые показатели для арок мезо-, ре- и протрузионного типа составляли соответственно 17,73±0,66; 17,20±0,73 и 19,16±0,67 мм без достоверных различий между всеми показателями (р ˃ 0,05).
Таким образом, метод Хаулея может быть использован для определения радиуса малого круга только при мезотрузионных вариантах верхних зубных дуг и протрузионных типах нижних арок.
При расчете радиуса с использованием модифицированного метода Хаулея и числа π было установлено, что радиус в среднем по группе с мезотрузионными вариантами зубных арок составил для верхней челюсти 22,04±0,62 мм. При ретрузионных вариантах дуг радиус окружности составлял 21,27±0,43 мм. В то же время при расчете для протрузионного типа радиус составлял 23,21±0,94 мм. На нижней челюсти исследуемые показатели для арок мезо-, ре- и протрузионного типа составляли соответственно 16,94±0,63; 16,44±0,70 и 18,30±0,64 мм без достоверных различий между всеми показателями (р ˃ 0,05). Таким образом, модифицированный метод Хаулея также может быть использован для определения радиуса малого круга только при мезотрузионных вариантах верхних зубных дуг и протрузионных типах нижних арок.
При расчете радиуса с использованием различий между шириной и глубиной переднего сектора (метод Ярадайкиной) было установлено, что радиус в среднем по группе с мезотрузионными вариантами зубных арок составил для верхней челюсти 25,01±0,68 мм и превышал значения контрольных цифр на 1,69±0,21 мм. При ретрузионных вариантах дуг радиус окружности составлял 25,81±0,93 мм и его значения были близки к фактической величине контрольных цифр. В то же время при расчете для протрузионного типа радиус составлял 22,93±0,99 мм, отклонение от контрольных цифр превышало 2,68±0,18 мм. На нижней челюсти исследуемые показатели для арок мезо-, ре- и протрузионного типа составляли соответственно 20,32±0,91; 20,84±1,03 и 19,73±0,72 мм без достоверных различий между всеми показателями (р ˃ 0,05). Таким образом, метод Ярадайкиной может быть использован для определения радиуса малого круга только при ретрузионных вариантах верхних зубных дуг, а также при мезотрузионных и протрузионных типах нижних арок.
При расчете радиуса с учетом закономерностей геометрии круга и параметров переднего сектора дуги было установлено, что радиус в среднем по группе с мезотрузионными вариантами зубных арок составил для верхней челюсти 23,19±0,73 мм и превышал значения контрольных цифр всего на 0,12±0,05 мм. При ретрузионных вариантах дуг радиус окружности составлял 25,81±1,19 мм, а при расчете для протрузионного типа радиус был 20,23±0,80 мм и показатели полностью соответствовали контрольным показателям. На нижней челюсти исследуемые показатели для арок мезо-, ре- и протрузионного типа составляли соответственно 21,55±1,12; 25,05±1,11 и 18,55±0,61 мм без достоверных различий с контрольными показателями (р ˃ 0,05). Таким образом, метод расчета радиуса с учетом закономерностей геометрии круга и параметров переднего сектора может быть использован для определения радиуса малого круга при всех трузионных вариантах верхних и нижних зубных дуг.
Заключение
Таким образом, предложен метод фотостатического исследования зубных дуг, который использовался при определении контрольных значений зубных дуг физиологической нормы. Метод Хаулея может быть использован для определения радиуса малого круга только при мезотрузионных вариантах верхних зубных дуг и протрузионных типах нижних арок. Метод расчета радиуса с учетом закономерностей геометрии круга и параметров переднего сектора может быть использован для определения радиуса малого круга при всех трузионных вариантах верхних и нижних зубных дуг, что может быть использовано в клинической ортодонтии при диагностике аномалий зубных дуг.
Библиографическая ссылка
Ягупова В.Т., Дмитриенко Д.С., Дмитриенко Т.Д., Ягупов П.П. МЕТОДЫ ОПРЕДЕЛЕНИЯ РАДИУСА ОКРУЖНОСТИ ДЛЯ РАСПОЛОЖЕНИЯ ПЕРЕДНИХ ЗУБОВ И ВОЗМОЖНОСТИ ИХ ИСПОЛЬЗОВАНИЯ В КЛИНИЧЕСКОЙ ОРТОДОНТИИ // Научное обозрение. Медицинские науки. 2023. № 2. С. 27-32;URL: https://science-medicine.ru/ru/article/view?id=1325 (дата обращения: 09.02.2026).
DOI: https://doi.org/10.17513/srms.1325
 science-review.ru
science-review.ru